Day 15:

剩下的團友加油，一起堅持到day30

希望瀏覽數可以多點啦，更多人看我的教學後有所增長
今天説的Python sympy比較複雜，那麼便開始吧。

什麼是 sympy

SymPy是用於符號計算的Python函式庫。它提供了許多功能強大的工具，用於解決代數、微積分、離散數學等領域的問題。

Sympy的應用

它可以計算微積分，解方程式，計算其他有關數學的公式。並可應用在物理、工程、教育、科學和研究。

由於這個模組是python內置的模組，不需要另外安裝。

範例1

第一個例子是儲存X為代數，並儲存一條方程式，在終端機註冊整理後的方程式。

import sympy as sp

x = sp.Symbol('x')
print(x+ x+x +10)

執行結果:

>> 3*x + 10

類別

這裏我們也做一個簡單的介紹，sp.symbol儲存後的值是一個類別，代表他有很多不同的功能。

import sympy as sp

x = sp.Symbol('x')
print(type(x))

執行結果:

>> <class 'sympy.core.symbol.Symbol'>

代入數字

這個先介紹一條簡單的方程式，並通過代入數字來取得答案，下例是一個簡單的範例:

import sympy as sp

x = sp.Symbol('x')
z = sp.Symbol('z')

equation = 5*x - 2*z
result = equation.subs({x:1, z:2}) #代入數字

print(f"5x-2z is {result}")

執行結果:

>> 5x-2z is 1

一元一次方程式

下面的例子是一元一次方程式:

這個是今次要計算的方程式
4x+2=10
4x+2-10=0

請記得，要把數字放到右邊，代數放到另外左邊。

import sympy as sp

x = sp.Symbol("x")

#4x+2=10
#4x+2-10=0
equation = 4*x+2-10

print(sp.solve(equation))

執行結果:

>> [2]

回傳的答案是一個列表，他可以用作儲存幾個不同的代數。

另外一個例子:

import sympy as sp

x = sp.Symbol("x")

equation =  x**2 + 5*x

print(sp.solve(equation))

執行結果:

>> [-5, 0]

繪圖

在數學課時，有一個方法是利用畫圖去取得代數的答案，sympy也有一樣的功能，利用matplotlib來繪畫出圖，下例是一個簡單的例子:

import sympy as sp
from sympy.plotting import plot

x = sp.Symbol("x")

eq1 = 3*x+10
eq2 = 4*x+15

line = plot(eq1,eq2,(x,-10,10),legend=True)

執行結果: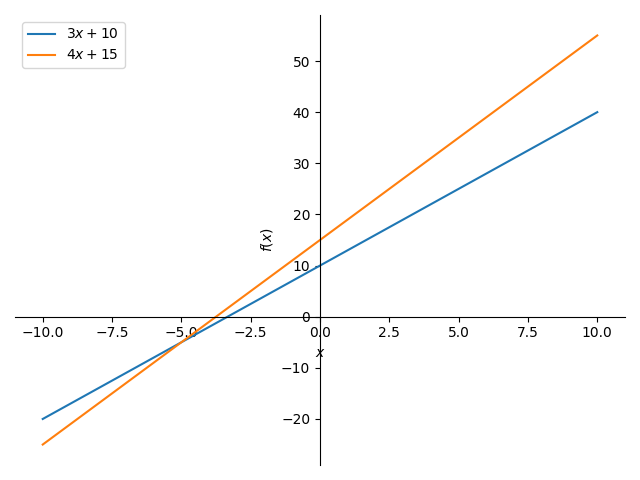

line = plot(eq1,eq2,(x,-10,10),legend=True)

Legend為matplotlob的函數，如果不清楚可以去看看我之前對matplot的介紹。
第一個函數是放入第一條線，第二個函數字放入第二條線，但是這兩條線可以無限延伸，所以要在第三個函數中加入起點及終點。

今天的內容覺得很有趣，如果覺得我的文章對你有幫助或有更好的建議，可以追蹤我和不妨在留言區提出，我們明天再見。

reference:
https://poe.com